Konzentrizität

Was ist Konzentrizität?

Die Konzentrizität bezieht sich auf das Konzept von Kreisen, Ellipsen oder anderen geometrischen Figuren, die sich innerhalb eines gemeinsamen Zentrums befinden. In der Mathematik und Geometrie ist Konzentrizität ein fundamentales Konzept, das in verschiedenen Anwendungsbereichen von großer Bedeutung ist. Sie findet Anwendung in Bereichen wie Geometrie, Analysis, Physik, Ingenieurwissenschaften und sogar in der Kunst.

Grundbegriffe

Zentrum: Das Zentrum ist der Punkt, der die Mitte einer geometrischen Figur darstellt. Bei konzentrischen Figuren teilen sie alle dasselbe Zentrum.

Kreis: Ein Kreis ist eine geschlossene Kurve, bei der alle Punkte auf der Kurve denselben Abstand, den sogenannten Radius, zum Zentrum haben. Bei konzentrischen Kreisen haben sie denselben Mittelpunkt, aber unterschiedliche Radien.

Ellipsen: Eine Ellipse ist eine geschlossene Kurve, bei der die Summe der Abstände zu zwei bestimmten Punkten, den Brennpunkten, für jeden Punkt auf der Kurve konstant ist. Konzentrische Ellipsen teilen sich dieselben Brennpunkte.

Konzentrische Kreise und Ellipsen: Konzentrische Kreise oder Ellipsen sind solche, die denselben Mittelpunkt haben, aber unterschiedliche Radien oder Halbachsen aufweisen.

Wie misst man Konzentrizität?

Die Messung der Konzentrizität hängt von der Art der geometrischen Figuren ab, die betrachtet werden, ob es sich um Kreise, Ellipsen oder andere Formen handelt. Hier sind einige allgemeine Methoden zur Messung der Konzentrizität:

1. Kreise: Wenn Sie konzentrische Kreise haben, die denselben Mittelpunkt teilen, aber unterschiedliche Radien haben, können Sie die Konzentrizität mithilfe von Messungen durchführen:

• Radienmessung: Messen Sie die Radien der konzentrischen Kreise an mehreren Stellen entlang der Kreisumfangs. Vergleichen Sie die gemessenen Radien und überprüfen Sie, ob die Unterschiede akzeptabel sind. Je geringer die Abweichung der Radien, desto konzentrischer sind die Kreise.

2. Ellipsen: Für konzentrische Ellipsen, die denselben Zentrums- und Brennpunkt teilen, jedoch unterschiedliche Halbachsenlängen haben, können Sie die Konzentrizität folgendermaßen messen:

• Halbachsenmessung: Messen Sie die Halbachsenlängen (große und kleine Halbachse) der konzentrischen Ellipsen an mehreren Stellen. Vergleichen Sie die gemessenen Längen und überprüfen Sie die Abweichungen. Geringere Unterschiede in den Halbachsenlängen deuten auf höhere Konzentrizität hin.

3. Technische Messgeräte: In vielen technischen Anwendungen, insbesondere in der Fertigung, werden spezialisierte Messgeräte verwendet, um die Konzentrizität von Objekten genau zu messen. Dazu gehören Koordinatenmessgeräte (CMMs), optische Messsysteme und Laserinterferometer. Diese Geräte können präzise Messungen der Position und Form von Objekten durchführen und Abweichungen von der idealen Konzentrizität identifizieren.

4. Software und Bildverarbeitung: In einigen Fällen kann die Konzentrizität mithilfe von Bildverarbeitungssoftware analysiert werden. Indem Bilder von den zu untersuchenden Objekten erfasst werden, kann die Software die Formen messen, die Positionen von Zentren und Brennpunkten bestimmen und Abweichungen berechnen.

Wenn Sie die Konzentrizität messen wollen, empfiehlt es sich sehr präzise zu sein, insbesondere wenn enge Toleranzen erforderlich sind. Die Wahl der Methode hängt von den spezifischen Anforderungen der Anwendung ab, sowie von den verfügbaren Werkzeugen und Ressourcen. In industriellen und wissenschaftlichen Umgebungen können spezialisierte Messgeräte und Software eingesetzt werden, während in einfacheren Fällen manuelle Messungen ausreichend sein können.

Konzentrizität: Anwendungsgebiete

Geometrie und Zeichnen: Konzentrische Kreise oder Ellipsen werden oft verwendet, um visuell ansprechende Muster zu erstellen oder um Objekte in technischen Zeichnungen darzustellen.

Elektrotechnik: In der Elektrotechnik werden konzentrische Leiter verwendet, um elektrische Felder zu erzeugen oder abzuschirmen, beispielsweise in Koaxialkabeln.

Optik: Konzentrische Ringe werden in der Optik verwendet, um Beugungsmuster oder Interferenzmuster zu erzeugen und bestimmte Eigenschaften von Licht zu untersuchen.

Architektur und Design: Konzentrische Muster werden oft in der Architektur und im Design verwendet, um visuelle Ausgewogenheit und Harmonie zu erzeugen.

Mechanik: In der Mechanik können konzentrische Ringe in Bauteilen verwendet werden, um Kräfte gleichmäßig zu verteilen oder um Drehbewegungen zu ermöglichen.

Beispiel für Konzentrizität

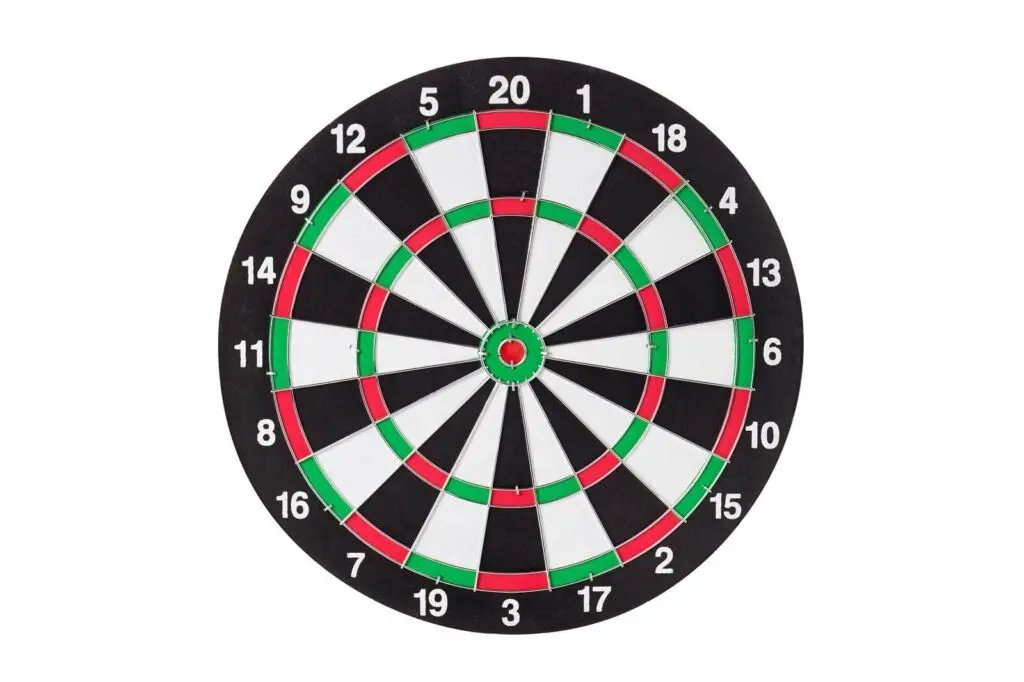
Ein häufig verwendetes Konzentrizität Beispiel sind die Ringe auf einer Zielscheibe, wie sie im Bogenschießen oder Schießsport verwendet werden. Die Konzentrizität der Ringe auf der Zielscheibe verdeutlicht das Konzept der geometrischen Figuren mit demselben Zentrum, aber unterschiedlichen Radien.

Stellen Sie sich eine Zielscheibe vor, die aus mehreren konzentrischen Ringen besteht. Jeder Ring hat denselben Mittelpunkt, aber unterschiedliche Radien, was bedeutet, dass die Ringe innerhalb des gleichen Zentrums liegen. Die äußeren Ringe haben größere Radien, während die inneren Ringe kleinere Radien haben. Die verschiedenen Ringe repräsentieren unterschiedliche Wertigkeiten oder Punkte, je nachdem, wie nahe sie dem Zentrum sind. Die Ringmitte, die mit dem Mittelpunkt der Zielscheibe zusammenfällt, wird oft als “Bullseye” bezeichnet und ist normalerweise der Bereich mit der höchsten Punktzahl.

Konzentrizität und Koaxialität: Unterschiede und Anwendungen

Sowohl Koaxialität als auch Konzentrizität sind Begriffe aus der Geometrie und werden oft in verschiedenen technischen und wissenschaftlichen Kontexten verwendet. Sie beschreiben jedoch unterschiedliche Beziehungen zwischen geometrischen Objekten. Hier sind die Unterschiede und Anwendungen von Koaxialität und Konzentrizität:

Konzentrizität

• Konzentrizität bezieht sich auf die Anordnung von geometrischen Figuren, die denselben Mittelpunkt teilen, jedoch unterschiedliche Radien oder Abstände vom Mittelpunkt haben.
• Ein Beispiel für konzentrische Objekte sind Kreise oder Ellipsen, die sich innerhalb derselben zentralen Position befinden, aber unterschiedliche Größen haben.
• Konzentrizität wird häufig in der Geometrie, Optik, Elektrotechnik und Kunst verwendet, um visuell ansprechende Muster zu erstellen, elektrische Felder zu erzeugen oder ästhetisch ansprechende Designs zu schaffen.

Koaxialität

• Koaxialität bezieht sich auf die Ausrichtung von Objekten entlang einer gemeinsamen Achse.
• Ein typisches Beispiel für koaxiale Objekte sind Koaxialkabel, bei denen der Innenleiter und der Außenleiter entlang derselben Achse verlaufen.
• Koaxialität wird in der Elektrotechnik, Telekommunikation und Datenübertragung verwendet, um Signale zu übertragen und Störeinflüsse zu minimieren.

Anwendungen

Konzentrizität: Wenn es darum geht, geometrische Figuren mit demselben Zentrum zu verwenden, aber unterschiedliche Größen oder Formen zu haben, ist die Konzentrizität von Bedeutung. Dies kann in der Kunst verwendet werden, um visuell ansprechende Muster zu erstellen, oder in technischen Zeichnungen, um verschiedene Schichten oder Komponenten darzustellen.

Koaxialität: Koaxiale Konfigurationen sind wichtig, wenn eine präzise Übertragung von Signalen erforderlich ist. Koaxialkabel werden in Telekommunikation, Fernsehen und Internetverbindungen verwendet, um Daten mit minimaler Signalverlust und Interferenz zu übertragen. Koaxiale Anordnungen finden auch in der Mikroelektronik Anwendung, um elektrische Verbindungen zwischen verschiedenen Schichten eines Mikrochips herzustellen.